Как раскроить конус из металла?
Как согнуть конус из металла своими руками
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса
Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Колпак на дымоход своими руками

Хозяева домов зачастую прибегают к использованию элементов в виде различных колпаков и зонтов, служащих, как это кажется на первый взгляд, для украшения дымовых труб. В то же время такие насадки не только улучшают эстетическое восприятие строения, но и обеспечивают полезную функциональность. Обычно так называемый козырек для дымохода изготавливается собственными силами, так как для этого не требуется серьезных знаний и умений. Хотя наряду с простой конструкцией этих элементов встречаются достаточно замысловатые поделки, которые проблематично соорудить без соответствующего опыта.
Конструктивные особенности
Колпак на дымоход представляет собой устройство, предназначенное для защиты трубы от попадания влаги. Внешний вид таких козырьков может быть различен, что имеет зависимость как от предпочтений хозяина дома, так и от конфигурации трубы.
Колпаки на трубу дымохода включают в себя:
- зонтик – устанавливаемая на вершине колпака защита от осадков, посторонних предметов и проникновения птиц, внешний вид которой имеет форму пирамиды, конуса или соответствует другой геометрии;
- фартук – часть колпака, отвечающая за защиту верха трубы от стекающей с зонтика воды. Обычно установка этого элемента производится при оснащении прямоугольной или квадратной трубы. В результате гарантируется увеличение срока службы дымохода, так как удается практически исключить вероятность появления коррозии и грибка;
- кронштейны – крепежные элементы, представляющие собой металлические полоски, которые позволяют соединить козырек и фартук. Непосредственное крепление в данном случае производится за счет использования сварки.
Имейте в виду! Собрать колпак для дымохода вполне реально самому, но только в том случае, если вы хотите установить достаточно простой флюгарок. Модели, отличающиеся большей сложностью в плане конструктивных особенностей, гораздо выгоднее заказать или купить.
При наличии выбора лучше всего отдать предпочтение тем моделям, которые оборудованы открывающейся крышкой. Это позволит проводить профилактический осмотр дымохода и его чистку без каких-либо проблем, что связано с комфортом доступа.
Колпак на дымоход долгого срока использования может быть изготовлен только из железа, устойчивого к коррозии: оцинкованная сталь, алюминий и медь. В последнем случае предлагаемый металл обладает ярко выраженным декоративным характером, так как его переливы на солнце могут придать вашем дому определенную респектабельность.
Одевают оголовок на трубу дымохода чтобы гасить искры. Это одно из его предназначений. Поэтому качество железа должно быть хорошим, тем самым оно долго не прогорит.
В связи с тем, что дымоходы отличаются разнообразием форм и размеров, производители колпаков также предлагают широкий ассортимент продукции. Если вы решите украсить свое жилище и продлить срок жизни дымохода, то придется выбирать среди большого ассортимента флюгарок:
- Стандартные – зонт на дымоход в виде пирамидки, для изготовления которой используется листовой металл, а крепление к фартуку осуществляется посредством кронштейнов.
- Четырехскатные – устанавливается преимущественно на прямоугольные трубы, выполненные из кирпича. По форме соотносится с вальмовой крышей с четырьмя скатами.
- С полукруглым зонтиком – визуально отличается красотой, но обеспечивает недостаточную тягу. Преимущественно используется для установки на дымоходах домов, которые построены по европейским стандартам.
- Плоские – часто можно встретить на зданиях в стиле модерн. Имеет прямоугольную форму и отличается таким недостатком, как повышенная нагрузка на кронштейны, что в некоторых случаях приводит к их деформации. Это связано с плоской крышей колпака, которая не дает возможность скатываться снегу. Данный факт определяет возникновение упомянутой проблемы.
- Круглые с конусообразным зонтиком – модели без капельника, устанавливаемые на выполненные из нержавейки дымоходы круглого сечения.
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Виды вальцевания
К основным видам вальцовки относятся следующие:
- Вальцевание труб (развальцовка) — применяется для изменения радиуса трубы.
- Вальцовка листового металла
— процедура сгибания листа металла в радиус.
Вальцовка труб осуществляется на трубогибных станках, которые способны выполнить вальцевание труб диаметром до 30 см. На таком же оборудовании обрабатываются уголки, швеллеры и прочие детали.
Вальцевание в радиус применяется для нержавеющих, черных, оцинкованных металлов различной толщины: стали, алюминия, меди. Для листов с толщиной свыше 10 мм требуется разогрев. Металлические листы до 10 мм толщиной сгибаются в холодном состоянии. Один из более сложных технологических процессов вальцевания листового металла
— это изготовление конусов. Также у нас имеется оборудование, на котором производятся конические и цилиндрические обечайки.
Если вам требуется вальцовка листового металла в Москве
— наша компания готова выполнить услуги под заказ качественно, на высоком профессиональном уровне. Мастера обладают колоссальным опытом и изготавливают детали с максимально точным радиусом. Они досконально знают принцип работы оборудования, скрупулезно соблюдают технологию, придерживаются всех нюансов обработки металла.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
- Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Соединяем точки A, B, C плавной линией.





Основание конуса
Чтобы узнать радиус основания конусного каркаса, линейкой производят измерение диаметра нижней части заготовки, представляющую собой бумажную (картонную) боковую поверхность.

Для большей точности линейку прикладывают к краям заготовки и измеряют расстояние в двух перпендикулярных направлениях. Вычисляют среднее значение диаметра и делят пополам. В итоге получают величину радиуса основания бумажного конуса.
Как раскроить конус из металла?
Развертка конуса. Построение развертки конуса

- Расчет развертки конуса.
Поверхность конуса состоит из боковой поверхности и поверхности основания.
Расчет развертки конуса.
Возьмем вертикальную и горизонтальную проекции конуса (рис. 1, а). Вертикальная проекция конуса будет иметь вид треугольника, основание которого равно диаметру окружности, а стороны равны образующей конуса. Горизонтальная проекция конуса будет изображаться окружностью. Если задана высота конуса Н, то длина образующей определяется по формуле:
т. е. как гипотенуза прямоугольного треугольника.
Обвернем картоном поверхность конуса. Развернув картон снова в одну плоскость (рис. 1, б), получим сектор, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса. Полную развертку боковой поверхности конуса выполняют следующим образом.
Рис. 1. Развертка конуса:
а — проекция; б — развертка.
Угол развертки конуса.
Принимая за радиус образующую конуса (рис. 1, б), на металле вычерчивают дугу, на которой затем откладывают отрезок дуги КМ, равный длине окружности основания конуса 2 π r. Длине дуги в 2 π r соответствует угол α, величина которого определяется по формуле:
г — радиус окружности основания конуса;
l — длина образующей конуса.
Построение развертки сводится к следующему. На длине ранее вычерченной дуги откладывается не часть дуги КМ, что практически является невозможным, а хорда, соединяющая концы этой дуги и соответствующая углу α. Величина хорды для заданного угла находится в справочнике или проставляется на чертеже.
Найденные точки КМ соединяются с центром окружности. Круговой сектор, полученный в результате построения, будет развернутой боковой поверхностью конуса.
Как раскроить конус из металла?

07 Дек 2013
Рубрика: Механика | 75 комментариев
За последнее время ко мне было несколько обращений от читателей блога за помощью в решении одной и той же задачи: как при работе на трехвалковых листогибочных вальцах и профилегибах определить окончательное местоположение среднего ролика (валка)…
…относительно положения крайних роликов (валков), которое обеспечит гибку (вальцовку) заготовки с определенным заданным необходимым радиусом? Ответ на этот вопрос позволит повысить производительность труда при гибке металла за счет уменьшения количества прогонов заготовки до момента получения годной детали.
В этой статье вы найдете теоретическое решение поставленной задачи. Сразу оговорюсь – на практике я этот расчет не применял и, соответственно, не проверял результативность предлагаемого метода. Однако я уверен, что в определенных случаях гибка металла может быть выполнена гораздо быстрее при использовании этой методики, чем обычно.
Чаще всего в обычной практике окончательное местоположение подвижного центрального ролика (валка) и количество проходов до получения годной детали определяется «методом тыка». После длительной (или не очень) отработки технологического процесса на пробной детали определяют координату положения центрального ролика (валка), которую и используют при дальнейших перенастройках вальцев, изготавливая партию этих деталей.
Метод удобен, прост и хорош при значительном количестве одинаковых деталей – то есть при серийном производстве. При единичном или «очень мелкосерийном» производстве, когда необходимо гнуть разные профили или листы разной толщины разными радиусами, потери времени на настройку «методом тыка» становятся катастрофически огромными. Особенно эти потери заметны при гибке длинных (8…11м) заготовок! Пока сделаешь проход…, пока проведешь замеры…, пока перестроишь положение ролика (валка)… — и все сначала! И так десяток раз.
Расчет в Excel местоположения подвижного среднего ролика
Запускаем программу MS Excel или программу OOo Calc, и начинаем работу!
С общими правилами форматирования электронных таблиц, которые применяются в статьях блога, можно ознакомитьсяздесь.
Прежде всего, хочу заметить, что листогибочные вальцы и профилегибы разных моделей могут иметь подвижные крайние ролики (валки), а могут — подвижный средний ролик (валок). Однако для нашей задачи это не имеет принципиального значения.
На рисунке, расположенном ниже изображена расчетная схема к задаче.
Вальцуемая деталь в начале процесса лежит на двух крайних роликах (валках), имеющих диаметр D. Средний ролик (валок) диаметром d подводится до касания с верхом заготовки.
Далее средний ролик (валок) опускается вниз на расстояние равное расчетному размеру H, включается привод вращения роликов, заготовка прокатывается, производится гибка металла, и на выходе получается деталь с заданным радиусом изгиба R! Осталось дело за малым – правильно, быстро и точно научиться рассчитывать размерH. Этим и займемся.
Исходные данные:
1. Диаметр подвижного верхнего ролика (валка) /справочно/ d в мм записываем
в ячейку D3: 120
2. Диаметр опорных с приводом вращения крайних роликов (валков) D в мм пишем
в ячейку D4: 150
3. Расстояние между осями опорных крайних роликов (валков) A в мм вводим
в ячейку D5: 500
4. Высоту сечения детали h в мм заносим
в ячейку D6: 36
5. Внутренний радиус изгиба детали по чертежу R в мм заносим
в ячейку D7: 600
Расчеты и действия:
6. Вычисляем расчетную вертикальную подачу верхнего ролика (валка)Hрасч в мм без учета пружинения
в ячейке D9: =D4/2+D6+D7- ((D4/2+D6+D7)2- (D5/2)2)(½)=45,4
Hрасч=D/2+h+R— ((D/2+h+R)2- (A/2)2)(½)
7. Настраиваем вальцы на этот размер Hрасч и делаем первый прогон заготовки. Измеряем или высчитываем по хорде и высоте сегмента получившийся в результате внутренний радиус, который обозначим Rи записываем полученное значение в мм
в ячейку D10: 655
8. Вычисляем какой должна была бы быть расчетная теоретическая вертикальная подача верхнего ролика (валка)H0расч в мм для изготовления детали с радиусом R без учета пружинения
в ячейке D11: =D4/2+D6+D10- ((D4/2+D6+D10)2- (D5/2)2)(½)=41,9
H0расч=D/2+h+ R0— ((D/2+h+ R0)2- (A/2)2)(½)
9. Но деталь с внутренним радиусом изгиба R получилась при опущенном верхнем валке на размер Hрасч, а не H0расч. Считаем поправку на обратное пружинение xв мм
в ячейке D12: =D9-D11=3,5
x=Hрасч — H0расч
10. Так как радиусы R и R имеют близкие размеры, то можно с достаточной степенью точности принять эту же величину поправки x для определения окончательного фактического расстояния H, на которое необходимо подать вниз верхний ролик (валок) для получения на вальцованной детали внутреннего радиуса R.
Вычисляем окончательную расчетную вертикальную подачу верхнего ролика (валка)Hв мм c учетом пружинения
в ячейке D13: =D9+D12=48,9
Расчет заготовки выкройки для усеченного конуса
Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции.
Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.
В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения.
Отсюда Р = D x H / (D-Dm).
Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей. Рассчитать развертку заготовки как бы для полного конуса, а затем «вычесть» из нее развертку его верхней, ненужной нам части. А можем рассчитать непосредственно радиусы заготовки.
Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.
Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2.
Теперь осталось рассчитать угол сектора, который надо вырезать.
Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов.
Т.е. Х / 360 = 3,14 x D / 6.28 x Rz
Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.
Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм.
Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм
По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)2 + 6002 = 618,5 мм
По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)2 + (200/2)2 = 364 мм.
Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса.
На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест.
Константин Тимошенко © 31.07.2014 г.
Конус из жести
По просьбе зрителя моего канала показываю как вручную изготовить конус из оцинкованной жести. Так же в ролике задета вскользь тема пайки оцинковки. Буду рад если кому то будет полезным. ******************************************************************** Может кто захочет помочь каналу, ну и мне, в приобретении более-менее нормальной видео камеры: Qiwi кошелёк:+77772333954 WebMoney: доллары Z498528204892 рубли R222943899342 тенге K409267298200 Спасибо за понимание и поддержку!
Alex Petrovich: Хоть бы в мастерской прибрался!
умар Туманов: Насчет ребрышек. Если сперва прокрутит в одну сторону а потом в обратную их не бывает но это не на всех листах один сказал что если лист холоднокатанный их не избежать а на теплокатанном шикарно выходит. Как их определить и что это такой фиг его знает. В Чечне в основном липецкий лист и большая часть по такой методике крутится без ребрышек
Sangita Namdy: Большое спасибо, очень полезное видео!
G.G. TV-410: Здраствуйте Павел, ты молодец, спосибо за хорощий видоси.всегда ставлю палец вверх-но если можно покажи ка конус на шов. как сделать.–заране спосибо.
konon ogurzow: Вот мужик молодец какой))
Сергей Белов: дядьк,молодец!шли всех на хуй! все правельно сделал ребра не какой роли не сыграют,молодец!
Построение развертки конуса
Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.
Варианты построения развертки:
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
- Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
- Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5. - Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
- Соединяем точки A0, B0, C0 плавной линией.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Как сделать ровный конус из бумаги. Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса
Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.








Печать конусообразных стаканчиков на принтере
Самый простой вариант — это печать на сувенирном принтере с помощью поворотного устройства. Видео взято на канале Andrey Printcompany.
Печать на конусном бокале. UV-принтер
Промышленный вариант, высокоскоростная UV-печать на специализированных принтерах. Видео 3sixty CMYK UV-print on cone shaped product взято на канале ACG Fyrtal.
Высокоскоростная UV-печать на специализированных принтерах
Ещё один промышленный UV-принтер — Inkjet Cylinder Printing Machine – The X360. Видео взято на канале Inkcups.
Inkjet Cylinder Printing Machine – The X360

Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Бумажный или пластиковый стаканчик
Самый распространенный конический предмет, с которым сталкиваются абсолютно все люди — это стаканчик. Он может быть бумажным или пластиковым, с принтом или без, но неизменным остается одно — это форма! Коническая фома стаканчика была выбрана не просто так, она имеет неоспоримое преимущество перед цилиндрической.
Форма конуса позволяет вставлять один стаканчик в другой, тем самым получается сформировать компактную упаковку из десятков изделий. Форма цилиндра не позволяет этого сделать. Итак, подобная конусообразная форма делает удобнее хранение, транспортировку и реализацию стаканчиков.
Однако, при необходимости напечатать картинку на конусообразном предмете, возникают некоторые технические и дизайнерские сложности. Сразу обращаю ваше внимание, что стаканчик является усеченным конусом, и далее рассматриваемый способ подготовки принта для печати, будет основан именно на построении макета усеченного конуса и подходит для любых подобных предметов, например, для кружек латте.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
- Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Соединяем точки A, B, C плавной линией.
Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Гибка металла на вальцах
07 Дек 2013 Рубрика: Механика |
За последнее время ко мне было несколько обращений от читателей блога за помощью в решении одной и той же задачи: как при работе на трехвалковых листогибочных вальцах и профилегибах определить окончательное местоположение среднего ролика (валка)…
…относительно положения крайних роликов (валков), которое обеспечит гибку (вальцовку) заготовки с определенным заданным необходимым радиусом? Ответ на этот вопрос позволит повысить производительность труда при гибке металла за счет уменьшения количества прогонов заготовки до момента получения годной детали.
В этой статье вы найдете теоретическое
решение поставленной задачи. Сразу оговорюсь – на практике я этот расчет не применял и, соответственно, не проверял результативность предлагаемого метода. Однако я уверен, что в определенных случаях гибка металла может быть выполнена гораздо быстрее при использовании этой методики, чем обычно.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.

Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Технология гибки листового металла своими руками
В процессе строительства дома или дачи зачастую появляется необходимость в оборудовании водостоков, канализации, каркасов из металла.
При изготовлении подобных изделий необходимо придать плоской заготовке необходимую пространственную форму. Советы опытных мастеров, как загнуть лист металла в домашних условиях, позволят изготавливать конструкции хорошего качества, которые прослужат долгое время.
Технология гибки – основные сведения
Сгибание металла выполняют без сварочных швов, что позволяет избежать коррозии в дальнейшем и получить изделие повышенной прочности. Деформация не требует значительных усилий и выполняется, как правило, в холодном состоянии.
Исключение составляют твердые материалы, вроде дюрали или углеродистых сталей. Технология гибки листового металла разрабатывается соответственно поставленным задачам в таких вариантах, как:
Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки.
Иногда возникает задача – изготовить защитный зонт для вытяжной или печной трубы, вытяжной дефлектор для вентиляции и т.п. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами.
Начнем с простого варианта — развертка простого конуса. Проще всего объяснить принцип расчета выкройки на примере.
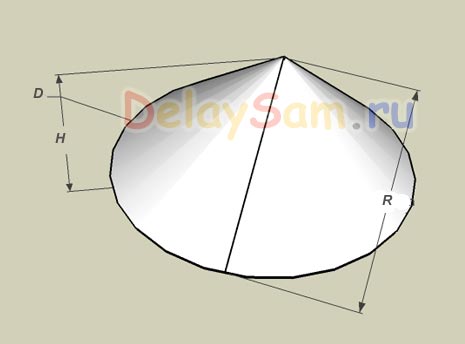
Допустим, нам надо изготовить конус диаметром D см и высотой H сантиметров. Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. Известны два параметра – диаметр и высота. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). Половина диаметра (радиус) и высота образуют прямоугольный треугольник. Поэтому:
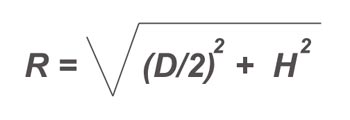
Итак, теперь мы знаем радиус заготовки и можем вырезать круг.
Вычислим угол сектора, который надо вырезать из круга. Рассуждаем следующим образом: Диаметр заготовки равен 2R, значит, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам нужно вырезать сегмент с длиной дуги равной разности этих длин. Применим правило соотношения. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.
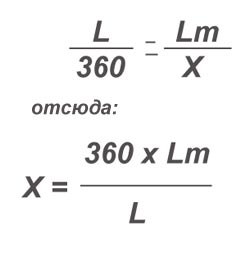
Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим путем вычитания 360 – Х.
Из круглой заготовки с радиусом R надо вырезать сектор с углом (360-Х). Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера.
Например: Нам нужен конус для зонта вытяжной трубы высотой (Н) 100 мм и диаметром (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности нужного нам конуса — 250 x 3,14 = 785 мм.
Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать надо сектор 360 – 281 = 79 градусов.

Расчет заготовки выкройки для усеченного конуса.
Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции.
Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.
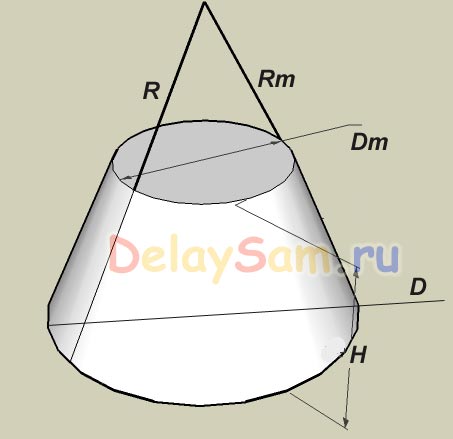
В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения.
Отсюда Р = D x H / (D-Dm).
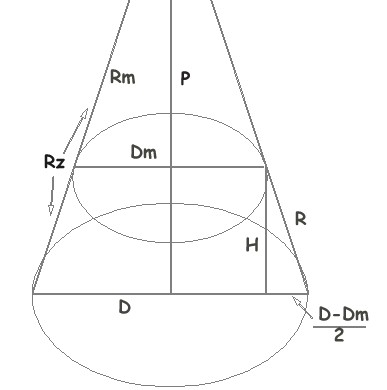
Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей. Рассчитать развертку заготовки как бы для полного конуса, а затем «вычесть» из нее развертку его верхней, ненужной нам части. А можем рассчитать непосредственно радиусы заготовки.
Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.
Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2.
Теперь осталось рассчитать угол сектора, который надо вырезать.
Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов.
Т.е. Х / 360 = 3,14 x D / 6.28 x Rz
Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.
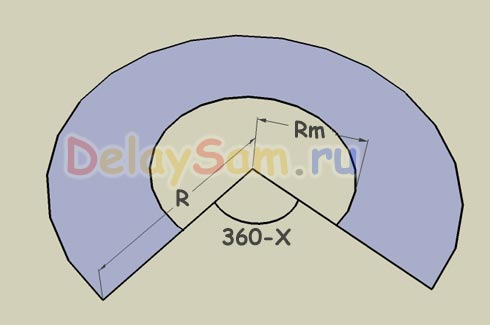
Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм.
Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм
По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)^2 + 6002 = 618,5 мм
По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)^2 + (200/2)^2 = 364 мм.
Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса.
На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест.
Константин Тимошенко © 31.07.2014 г.
Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки.
Иногда возникает задача – изготовить защитный зонт для вытяжной или печной трубы, вытяжной дефлектор для вентиляции и т.п. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами.
Начнем с простого варианта — развертка простого конуса. Проще всего объяснить принцип расчета выкройки на примере.

Допустим, нам надо изготовить конус диаметром D см и высотой H сантиметров. Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. Известны два параметра – диаметр и высота. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). Половина диаметра (радиус) и высота образуют прямоугольный треугольник. Поэтому:
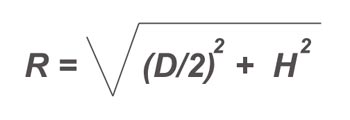
Итак, теперь мы знаем радиус заготовки и можем вырезать круг.
Вычислим угол сектора, который надо вырезать из круга. Рассуждаем следующим образом: Диаметр заготовки равен 2R, значит, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам нужно вырезать сегмент с длиной дуги равной разности этих длин. Применим правило соотношения. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.
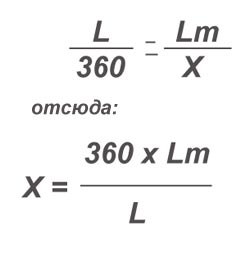
Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим путем вычитания 360 – Х.
Из круглой заготовки с радиусом R надо вырезать сектор с углом (360-Х). Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера.
Например: Нам нужен конус для зонта вытяжной трубы высотой (Н) 100 мм и диаметром (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности нужного нам конуса — 250 x 3,14 = 785 мм.
Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать надо сектор 360 – 281 = 79 градусов.

Расчет заготовки выкройки для усеченного конуса.
Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции.
Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.

В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения.
Отсюда Р = D x H / (D-Dm).

Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей. Рассчитать развертку заготовки как бы для полного конуса, а затем «вычесть» из нее развертку его верхней, ненужной нам части. А можем рассчитать непосредственно радиусы заготовки.
Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.
Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2.
Теперь осталось рассчитать угол сектора, который надо вырезать.
Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов.
Т.е. Х / 360 = 3,14 x D / 6.28 x Rz
Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.

Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм.
Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм
По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)^2 + 6002 = 618,5 мм
По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)^2 + (200/2)^2 = 364 мм.
Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса.
На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест.
Константин Тимошенко © 31.07.2014 г.