Интерференция зубьев на шестерне что это?

iSopromat.ru

При проектировании зубчатой передачи необходимо проверить геометрические показатели, которые могут привести к неудовлетворительной ее работе.

К ним относятся:

— коэффициент перекрытия. Коэффициентом перекрытия называется отношение дуги зацепления к шагу зацепления на той же окружности (дуга зацепления – это путь, проходимый точкой зуба по дуге окружности за время работы данной пары – на рисунке 39б показана дуга зацепления по основной окружности – b₁b₂).

Если дуга зацепления окажется меньше шага, то при выходе из зацепления одной пары зубьев следующая не вступит в зацепление. Нарушается преемственность в работе пар, передача работает с ударами и быстро выходит из строя. Поэтому коэффициент перекрытия должен быть больше или, в крайнем случае, равен единице.

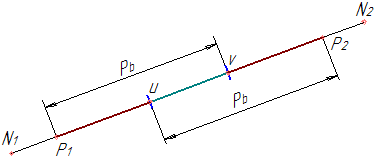
Чем больше коэффициент перекрытия, тем более плавной будет работа передачи. На основании третьего свойства эвольвенты рабочая часть линии зацепления Р₁Р₂ равна дуге зацепления на основной окружности (рисунок 39б), а расстояние между работающими профилями двух соседних зубьев, измеренное по линии зацепления равно основному шагу. Поэтому коэффициент перекрытия можно вычислить как отношение отрезка Р₁Р₂ к основному шагу р_В (рисунок 43):

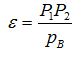
После преобразований получаем:

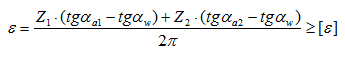
В этой формуле α_a1 и α_a2 – углы профиля на окружности вершин первого и второго колеса соответственно. Определяются через функцию косинуса:

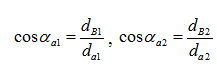
Рекомендуется принимать следующие значения допускаемого коэффициента перекрытия:

[ ε ]=1,05…1,1 – для неответственных передач,
[ ε ]=1,2 – для ответственных передач.

При нарезании колес стандартным инструментом реечного типа коэффициент перекрытия в цилиндрической передаче не может превышать значения 1,88. То есть в реальных передачах значения коэффициента перекрытия располагаются в интервале 1,05…1.8. Это означает, что какую-то часть времени работают две пары зубьев одновременно, какую-то – одна пара зубьев.

В тот момент времени, когда пара зубьев входит в зацепление в точке Р₁, предыдущая пара находится от нее на расстоянии основного шага в точке “v” линии зацепления (рисунок 43). С этого момента в зацеплении находятся две пары (и делят передаваемую нагрузку между собой). Когда предыдущая пара подойдет к точке Р₂, то следующая пара будет располагаться в точке» u” (на расстоянии основного шага от точки Р₂).

В следующий момент предыдущая пара выйдет из зацепления, а следующая войдет в зону ”uv” и будет воспринимать всю нагрузку целиком. Пока пара находится в зоне “uv” никакая другая пара находиться в зацеплении не будет. Поэтому эта часть линии зацепления называется зоной однопарного зацепления. Часть профиля, которая работает в зоне однопарного зацепления, является наиболее напряженной частью этого профиля.

Чем больше коэффициент перекрытия, тем меньше зона однопарного зацепления, тем большую часть времени в зацеплении находятся две пары зубьев.

— интерференция зубьев зубчатых колес. Профиль зуба состоит из двух характерных частей – из эвольвентной части, и переходной кривой, плавно сопрягающей эвольвентную часть с окружностью впадин (рисунок 44 а).

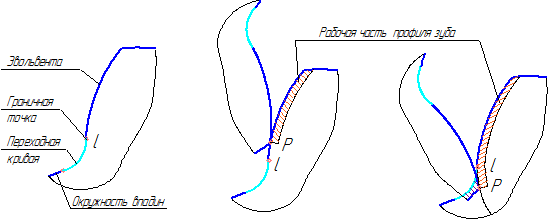
Если рабочая часть профиля располагается целиком на его эвольвентной части, то происходит нормальная работа зубьев без нарушения основного закона зацепления (рисунок 44 б). Если же нижняя точка Р рабочего участка окажется ближе к основной окружности, чем граничная точка l сопряжения эвольвенты с переходной кривой, то вершина зуба одного колеса будет стремиться к внедрению в переходную кривую второго (рисунок 44 в).

Вершина зуба одного колеса накладывается (на чертеже) на переходную кривую второго (как отмечалось выше, это явление называется интерференцией профилей). Нарушается основной закон зацепления, происходит заклинивание или поломка передачи. Интерференция отсутствует, если нижняя точка рабочего участка профиля зуба Р располагается на профиле выше граничной точки l .

Положение точки на эвольвенте можно задать через различные параметры (через диаметр, через угол профиля, через угол развернутости, через эвольвентный угол). Наиболее удобные формулы получаются через углы профиля в рассматриваемых точках (формула для определения угла профиля в граничной точке l приведена выше, формулы для определения угла профиля в точках Р₁ и Р₂ получаются из рассмотрения рисунка 39б):

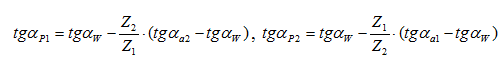
Условие отсутствия интерференции:

• на ножке зуба первого колеса
  
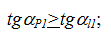
• на ножке зуба второго колеса
  
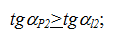
• заострение зубьев. Если расчетный диаметр вершин окажется больше диаметра окружности, на которой происходит пересечение встречных эвольвент, формирующих зуб, то фактический диаметр вершин окажется меньше расчетного (значит уменьшится коэффициент перекрытия), а зуб будет иметь острую вершину (рисунок 45а).

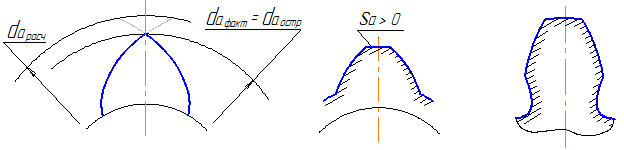
При приложении нагрузки к вершине будут возникать большие напряжения (теоретически площадь равна нулю), что приведет к смятию пластичного материала или к разрушению хрупкого материала у этой вершины. Поэтому при проектировании передачи необходимо обеспечить у зуба некоторую толщину на окружности вершин S_a>0 (рисунок 45 б).

При проверке на отсутствие заострения толщина зуба на окружности вершин сравнивается с допускаемой величиной:

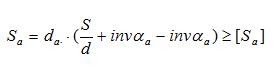
Рекомендуется принимать следующие значения допускаемой толщины зуба на окружности вершин:

[S_a]=0,25m – для пластичных материалов;
[S_a]=0,40m – для хрупких материалов;

— подрезание (подрез) зубьев. При определенных условиях инструмент начинает пересекать им же сформированную эвольвенту у основания зуба. Формируемая им переходная кривая в этом случае пересекает эвольвенту изнутри (а не плавно с ней сопрягается), а зуб становится более тонким (ослабленным) у основания. Это явление носит название подрезания или подреза зубьев (рисунок 45в).

Зубья с подрезом можно применять для несиловых передач, если оставшийся участок эвольвенты обеспечивает необходимый коэффициент перекрытия. Для силовых передач применять зубья с подрезом не рекомендуется. При применении стандартного инструмента реечного типа подрез зубьев происходит в том случае, когда верхняя точка прямолинейного участка профиля зуба рейки заходит за точку N линии зацепления (рисунок 41). Поэтому проверка на отсутствие очень простая:

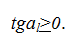
Вероятность подреза повышается с уменьшением числа зубьев колеса. Если изготавливать колеса стандартным инструментом реечного типа без применения смещения, то подрез будет наблюдаться у колес с числом зубьев меньше 17 (Z_min=17), и чем меньше число зубьев, тем более значительным будет подрез. Однако, если правильно подобрать коэффициент смещения, то колесо с любым число зубьев можно нарезать без подреза. Подрез у колеса с заданным числом зубьев будет отсутствовать, если коэффициент смещения будет не меньше минимального:

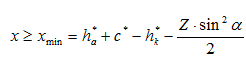
Влиять на все указанные геометрические показатели качества зацепления можно правильным выбором коэффициентов смещения. Для рационального выбора коэффициентов смещения при проектировании передачи разработаны так называемые блокирующие контуры.

Так как показатели описываются соответствующими математическими зависимостями, то их можно представить в виде линий в определенной системе координат. Совокупность этих линий в системе координат (x₁ – x₂ ) для определенной пары колес (z₁ – z₂) представляет собой замкнутый контур, отделяющий разрешенную зону для выбора коэффициентов смещения (x₁ и x₂) от запрещенной.

Этот замкнутый контур и называется блокирующим контуром. Он позволяет конструктору спроектировать бесчисленное количество работоспособных передач с одинаковыми числами зубьев колес, но с различными свойствами.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Интерференция — наложение профиля зуба одного колеса на профиль зуба другого при проектировании зацепления;

Подрезание – наложение профиля зуба инструмента на профиль зуба изготавливаемого колеса при нарезании зубьев.

Заклинивание – наложение профилей зубьев, но не при изготовлении, а при зацеплении колес.

Рассмотрим подробней явление подрезания. Так как параметры зуборезного инструмента стандартны, то при прочих равных условиях возможность подрезания ножки зуба определяется положением точки N, т.е. размерами колеса. Подрезание не происходит, когда точка контакта между производящей поверхностью инструмента и профилем зуба нарезаемого колеса находится правее точки N. Левее точки N эти поверхности будут не касаться друг друга, а пересекаться, что и приводит к подрезанию ножки зуба. Подрезание уменьшает эвольвентную часть профиля зуба колеса, ослабляет прочность зуба в опасном сечении и уменьшает коэффициент перекрытия.

Рассмотрим вопрос о наименьшем числе зубьев Z_min на колесе, при котором явление подрезания будут отсутствовать при нарезании зубьев рейкой с учетом смещения.

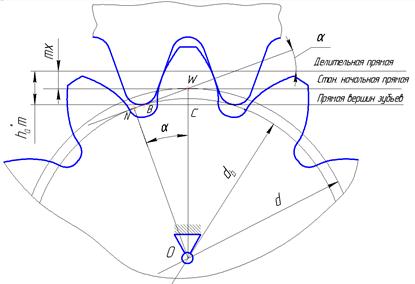По условию не подрезания, должно выполняться условие NW ≥ BW. Из треугольника ОNW можно выразить катет NW, используя модуль и число зубьев

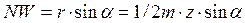
Из треугольника BWC можно найти гипотенузу BW, используя модуль,

высоту головки зуба и коэффициент смещения Рисунок 5 инструмента

≥

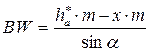
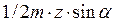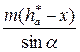
Отсюда число зубьев, которое можно нарезать реечным инструментом без подрезания ножки зуба, с учётом смещения будет равно

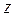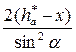= (3)

Минимальное число зубьев без смещения реечного инструмента и без подрезания ножки зуба, можно нарезать

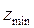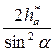==17,01 (4)

Используя выражение (3) и (4), можно определить минимальный коэффициент смещения, при котором не будет подрезания ножки зуба.

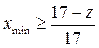
Основные способы исправления зубчатых колес (нарезание зубьев без подрезания). Из выражения (4) видно, что можно уменьшить коэффициент высоты головки зуба (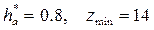) или увеличить угол профиля исходного контура a (a = 25 0 , z_min = 11). В том и другом случае инструмент будет не стандартным.

Смещение зуборезного инструмента меняет не только параметры зубчатых колес, но и зацепления в целом, поэтому при исправлении смещением, рассматривается суммарный коэффициент смещения (х_å).

Нормальное или нулевое зацепление, при котором х_å = 0, может быть в двух случаях – когда х₁ = х₂ = 0, т.е колеса не исправленные, и когда х₁ = -х₂. И в том и другом случае делительные и начальные окружности будут совпадать, т.е. a =a_w, а а =а_w(смотрите выражения (1) и (2)). При исправленных колесах это исправление будет называться высотным, так как изменяется высота головки и ножки зуба.

Положительное зацепление, при котором х_å > 0. В этом случае начальные окружности будут больше делительных и a a_w, а а > а_w .

В последних двух случаях такое исправление называется угловым.

Исследование интерференции зубьев в нагруженной волновой зубчатой передаче Текст научной статьи по специальности « Механика и машиностроение»

Аннотация научной статьи по механике и машиностроению, автор научной работы — Люминарский Станислав Евгеньевич, Люминарский Игорь Евгеньевич

При проектировании волновых зубчатых передач (ВЗП) актуальной является задача исключения интерференции зубьев в зацеплении гибкого и жесткого колес . Если интерференция достаточно большая, то при повороте генератора зубья гибкого и жесткого колес упираются поверхностями вершин. При этом жесткое колесо растягивается, а генератор волн сжимается. В результате этих деформаций при большой интерференции зубьев происходит проскок генератора. При этом зубья на входе в зацепление вначале упираются поверхностями вершин, а при дальнейшем повороте генератора соскакивают и зацепляют боковыми поверхностями. Такая работа передачи недопустима, так как она приводит к увеличению динамических нагрузок и износу вершин зубьев. Продукты износа засоряют смазку, что может привести к порче гибкого подшипника. Приведена методика определения максимального момента сопротивления M * c, при котором отсутствует интерференция зубьев . Представлены результаты теоретических исследований влияния различных геометрических параметров передачи на указанный момент M * c. Исследовано влияние квалитета точности деталей рассматриваемой ВЗП на интерференцию зубьев . Результаты исследования расширяют знания об интерференции зубьев в ВЗП.

Похожие темы научных работ по механике и машиностроению , автор научной работы — Люминарский Станислав Евгеньевич, Люминарский Игорь Евгеньевич

Analysis of meshing interference in a loaded harmonic drive

When designing harmonic drives it is important to avoid meshing interference of the flex spline and the circular spline . If the interference is significant, then the teeth of the flex and circular splines bear against the top lands of each other when the wave generator turns. At the same time, the rigid gear stretches and the wave generator contracts. As the result of these deformations at large meshing interference , the wave generator skips. First, the teeth bear against the top lands of each other and, as the wave generator turns further, come off and catch the side surfaces. The operation of the harmonic drive under such conditions is unacceptable as it leads to the increased dynamic loads and the wear of the top lands. The wear debris can clog the lubricant and cause damage to the flexible bearing. The article describes a method for determining the maximum torque M * c when meshing interference is absent. The results of the theoretical research into the influence of various geometrical parameters onto the specified torque M * c are presented. The relationship between the accuracy of the harmonic drive parts and the meshing interference is analyzed. The results presented in the article broaden knowledge about meshing interference in harmonic drives.

Текст научной работы на тему «Исследование интерференции зубьев в нагруженной волновой зубчатой передаче»

Исследование интерференции зубьев

в нагруженной волновой зубчатой передаче

С.Е. Люминарский1, И.Е. Люминарский2

1 МГТУ им. Н.Э. Баумана, 105005, Москва, Российская Федерация, 2-я Бауманская ул., д. 5, стр. 1

2 Московский государственный индустриальный университет, 115280, Москва, Российская Федерация, ул. Автозаводская, д. 16

Analysis of meshing interference in a loaded harmonic drive

S.E. Lyuminarsky1, I.E. Lyuminarsky2

1 BMSTU, 105005, Moscow, Russian Federation, 2nd Baumanskaya St., Bldg. 5, Block 1

2 Moscow State Industrial University, 115280, Moscow, Russian Federation, Avtozavodskaya St., Bldg. 16

e-mail: katjstas@mail.ru, lie260@mail.ru

При проектировании волновых зубчатых передач (ВЗП) актуальной является задача исключения интерференции зубьев в зацеплении гибкого и жесткого колес. Если интерференция достаточно большая, то при повороте генератора зубья гибкого и жесткого колес упираются поверхностями вершин. При этом жесткое колесо растягивается, а генератор волн сжимается. В результате этих деформаций при большой интерференции зубьев происходит проскок генератора. При этом зубья на входе в зацепление вначале упираются поверхностями вершин, а при дальнейшем повороте генератора соскакивают и зацепляют боковыми поверхностями. Такая работа передачи недопустима, так как она приводит к увеличению динамических нагрузок и износу вершин зубьев. Продукты износа засоряют смазку, что может привести к порче гибкого подшипника. Приведена методика определения максимального момента сопротивления MJ, при котором отсутствует интерференция зубьев. Представлены результаты теоретических исследований влияния различных геометрических параметров передачи на указанный момент М*. Исследовано влияние квалитета точности деталей рассматриваемой ВЗП на интерференцию зубьев. Результаты исследования расширяют знания об интерференции зубьев в ВЗП.

Ключевые слова: волновая зубчатая передача, гибкое колесо, жесткое колесо, интерференция зубьев, квалитет точности.

When designing harmonic drives it is important to avoid meshing interference of the flex spline and the circular spline. If the interference is significant, then the teeth of the flex and circular splines bear against the top lands of each other when the wave generator turns. At the same time, the rigid gear stretches and the wave generator contracts. As the result of these deformations at large meshing interference, the wave generator skips. First, the teeth bear against the top lands of each other and, as the wave generator turns further, come off and catch the side surfaces. The operation of the harmonic drive under such conditions is unacceptable as it leads to the increased dynamic loads and the wear of the top lands. The wear debris can clog the lubricant and cause damage to the flexible bearing. The article describes a method for determining the maximum torque M* when meshing interference is absent. The results of the theoretical research into the influence of various geometrical parameters onto the specified torque M* are presented. The relationship between the accura-

cy of the harmonic drive parts and the meshing interference is analyzed. The results presented in the article broaden knowledge about meshing interference in harmonic drives.

Keywords: harmonic drive, flex spline, circular spline, meshing interference, accuracy.

Перспективное направление развития электромеханических приводов — использование волновых зубчатых передач (ВЗП). Благодаря наличию гибкого элемента они позволяют получить большое передаточное число при малых габаритах, имеют большую нагрузочную способность и высокую кинематическую точность.

В настоящее время нагрузочную способность ВЗП определяют по условиям усталостной прочности гибкого колеса (ГК) и долговечности подшипников генератора волн [1-3]. Экспериментальные исследования и эксплуатация этих передач показывают, что волновые передачи выходят из строя не только из-за поломки ГК или генератора волн. Нарушение работоспособности может также наступать вследствие проскока генератора в результате интерференции зубьев на входе в зацепление [4-6]. Поэтому одним из важнейших факторов нормальной работы ВЗП является отсутствие интерференции зубьев.

Цель работы — определение для нагруженной ВЗП максимального момента М*, при котором отсутствует интерференция зубьев; исследование влияния геометрических параметров передачи и класса точности деталей на этот момент.

В волновой зубчатой передаче возможны два вида интерференции зубьев. Первый вид интерференции обусловлен контактом зубьев на переходных поверхностях гибкого и жесткого колес. В этом случае нарушается эвольвентный характер зацепления, что вызывает увеличение нагрузок на зубья, повышенный их износ и снижение КПД. Второй вид интерференции заключается в том, что на входе (или выходе) зацепления зазоры между боковыми поверхностями зубьев имеют отрицательные значения. При этом зубья начинают взаимодействовать не боковыми поверхностями, а поверхностями вершин в результате чего жесткое колесо (ЖК) растягивается, а генератор волн сжимается. При большой интерференции это приводит к проскоку. Момент на ведомом звене, при котором происходит проскок, принято называть предельным моментом.

Если интерференция зубьев 2-го рода небольшая, то проскока не будет. При входе в зацепление зубья вначале будут упираться поверхностями вершин, а при дальнейшем повороте генератора — соскакивать и зацепляться

боковыми поверхностями зубьев. Такая работа передачи недопустима, так как она обусловливает увеличение динамических нагрузок, износ боковых поверхностей зубьев, снижение КПД.

При проектировании первых ВЗП допускалась небольшая интерференция зубьев. Предполагалось, что после приработки интерференция исчезнет. Однако, как показала эксплуатация волновых передач, даже небольшая интерференция засоряет смазку и может привести к выходу их строя гибких подшипников.

Обычно при выборе параметров передачи проверяют отсутствие интерференции на холостом ходу. В работе [4] рассмотрены области существования основных параметров при нулевой нагрузке. В нагруженной передаче боковые зазоры изменяются, что может способствовать интерференции зубьев. Как показывают расчеты, при увеличении момента на выходном валу минимальный боковой зазор 5т;п при входе в зацепление уменьшается. Момент на выходном валу, при котором указанный зазор становится равным нулю, назовем моментом начала интерференции М*. При увеличении момента сопротивления Мс зазор 5т;п уменьшается. Следовательно, при Мс > М* в передаче происходит интерференция зубьев 2-го рода.

Математическая модель. В отличие от зубчатых передач с ЖК в ВЗП интерференция зависит от нагрузки, т. е. от момента на выходном валу. Поэтому для исследования интерференции необходим расчет силового взаимодействия элементов ВЗП. Силовой расчет волновых передач рассмотрен во многих работах. Однако в них силы взаимодействия элементов передачи приводятся к одной расчетной плоскости, т. е. не учитывается пространственный характер деформации элементов передачи. Изменение зазоров по длине зубчатого венца определяется приближенно, путем учета перекоса образующей оболочки ГК.

Для исследования интерференции зубьев в настоящей работе была использована математическая модель волновой передачи, в которой учитывается пространственный характер взаимодействия ее элементов [7, 8].

Исследуемая ВЗП с кулачковым генератором волн представлена на рис. 1. В расчетной модели ЖК 5 считается упругим, т. е. его деформация подчиняется закону Гука. Расчет узловых

зисных функций используются функции ик = 3ф к З (Sfc — площадь основания пирамиды). Базисные функции представляют собой шестиугольные пирамиды с единичным объемом и имеют размерность м-2.

Для составления разрешающей системы уравнений используется метод Бубнова — Га-леркина. В общем виде эта система записывается следующим образом:

Рис. 1. Волновая зубчатая передача: 1 — гибкий подшипник; 2 — крышка корпуса; 3 — корпус волнового редуктора; 4 — фланцевый двигатель; 5 — ЖК;

6 — ГК; 7 — наружное кольцо гибкого подшипника

податливостей ЖК выполнен методом конечных элементов. Жесткое колесо установлено с натягом в корпусе и из-за погрешности изготовления деталей может смещаться в плоскости вращения кулачка.

Гибкое колесо может взаимодействовать с ЖК по рабочим и нерабочим боковым поверхностям зубьев. При расчете оно заменяется ор-тотропной оболочкой с эквивалентными жест-костями в области зубчатого венца.

Наружное кольцо гибкого подшипника (НКГП) 7 не закреплено и уравновешивается силами, действующими со стороны ГК и тел качения. При расчете учитываются только нормальные силы взаимодействия поверхностей. Расчет узловых податливостей НКГП и ГК выполняется по линейной теории оболочек методом ортогональной прогонки. При расчете учитывается взаимодействие боковых поверхностей зубьев, внутренней поверхности ГК и наружной поверхности НКГП, внутренней поверхности НКГП и тел качения. Силы взаимодействия между поверхностями заменяются поверхностными силами с кусочно-линейным распределением [9]. Для этого все указанные поверхности разбиваются на треугольные области. Каждому узлу образованной сетки ставится в соответствие функция Куранта фkq2) [9], которая представляет собой шестиугольную пирамиду с единичной высотой. В качестве ба-

Проверка качества зацепления по геометрическим показателям

Для оценки спроектированной передачи используют следующие качественные показатели зацепления:

1) интерференция – явление, состоящее в том, что при рассмотрении теоретической картины зацепления часть пространства оказывается одновременно занятой двумя взаимодействующими зубьями. Зубья колеса защемляются во впадинах шестерни, что влечет за собой поломку зубьев или их усиленный износ;

2) подрезание зуба — срезание части поверхности у основания зуба обрабатываемого зубчатого колеса в результате интерференции зубьев при станочном зацеплении. Подрезание уменьшает эвольвантную часть профиля зуба колеса и ослабляет зуб у основания;

3) заострение зуба — явление, при котором пересечение двух симметричных боковых профилей зуба происходит ниже окружности вершин зубьев. В результате заострения высота зуба может умень­шиться, снижается и его прочность;

4) коэффициент перекрытия — это отношение угла перекрытия (угла поворота зубчатого колеса от положения входа зуба в зацепление до выхода из него) к угловому шагу зубьев. Он характеризует плавность и непрерывность работы передачи. Для непрерывности за­цепления необходимо, чтобы коэффициент перекрытия был не менее единицы. Плавность работы передачи тем выше, чем больше коэффи­циент перекрытия;

5) коэффициент скольжения учитывает влияние геометрических и кинематических факторов на величину проскальзывания профилей зубьев в процессе зацепления. Скольжение зубьев приводит к из­носу профилей и их заеданию (схватыванию металла). О качестве пе­редачи принято судить — по максимальным значениям коэффициентов скольжения, которые соответствуют зацеплению пары зубьев в точках А и В (см. рис.2) линии зацепления NN.Чем меньше коэффи­циент скольжения, тем меньший износ зуба;

6) коэффициент удельного давления учитывает влияние геомет­рии зубьев колес (радиусов кривизны их профилей) на контактную прочность и выкрашиваемость зубьев. Надо стремиться к тому, что­бы коэффициент удельного давления имел возможно наименьшее зна­чение (меньше единицы).

Проверка отсутствия интерференции зубьев

Условие отсутствия интерференции имеет вид

,

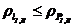где 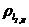— радиусы кривизны в граничной точке профиля зуба (см. рис.2);

— радиусы кривизны активного профиля зуба в нижней точке (см. рис.2)

Если в курсовом проекте для шестерни или колеса указанное условие не выполняется, то следует уменьшить (на 10¸20%) значения соответствующего коэффициента смещения ( и 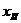) и расчет геометрически повторить.

Радиус кривизны активного профиля зуба в нижней точке

а) для шестерни ( в точке А на рис.2)

где — угол профиля у вершины зуба колеса

б) для колеса (в точке В на рис. 2)

где — угол профиля у вершины зуба шестерни

Для шестерни 4,17

Дата добавления: 2018-04-04 ; просмотров: 290 ; Мы поможем в написании вашей работы!

Проверка дополнительных условий при синтезе эвольвентного зацепления.

Из многих возможных дополнительных условий синте­за (ограничений), которые можно проверить по картине зацепле­ния, рассмотрим три условия: отсутствие заострения зубьев, отсутствие интерференции зубьев и обеспечение непрерывности взаимо­действия зубьев.

Заострение зуба получается, если точка T (см. рис.6.17) пересечения двух симметричных профилей располагается вблизи окружности вершин зубьев, и толщина зуба по этой окружности получается менее некоторой величины, например (0,1—0,15)m. Для устранения заострения зуба можно уменьшить радиус окруж­ности вершин или изменить коэффициенты смещения.

Интерференцией (наложением) зубьев называется явле­ние, состоящее в том, что при рассмотрении теоретической карти­ны зацепления часть пространства оказывается одновременно за­нятой двумя зубьями разных колес. Для внешнего эвольвентного зацепления условие отсутствия интерференции состоит в том, что взаимодействие зубьев должно происходить только на участке АВ, где обеспечивается касание зубьев.

Условие непрерывности взаимодействия зубьев состо­ит в том, что вторая пара взаимодействующих зубьев должна вой­ти в зацепление прежде, чем выйдет из зацепления первая пара. Если вращение колеса 1 (рис.6.18) происходит против хода часовой стрелки, то зуб входит в зацепление, когда его профиль пересека­ет линию зацепления в точке а и выходит из зацепления в точке b. Угол поворота зубчатого колеса от входа зуба в зацепление до вы­хода его из зацепления называется углом перекрытия колеса j_a. Отношение угла перекрытия колеса к его угловому шагу называ­ется коэффициентом перекрытия. Для колеса 1

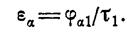(6.18)

Для непрерывности зацепления необходимо, чтобы угол пере­крытия был больше углового шага, т. е. e_a > 1.

По свойству образования эвольвенты дуга, которую проходит начальная точка эвольвенты от входа зуба в зацепление до выхода его из зацепления, равна длине активной линии зацепления ab. Следовательно, угол перекрытия для колеса 1 j_a1 = ab/r_b1

Подставляя значение угла перекрытия и углового шага в (6.18) получаем

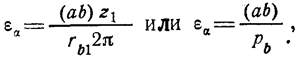(6.19) где р_b = pmcosa_w — шаг зубьев по основной окружности.

Формулу (6.19) можно получить также, если взять отношение угла перекрытия j_a2 для колеса 2 к его угловому шагу t₂.

Отрезок ab может быть вычислен из условия

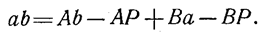
Подставляя значения указанных отрезков из треугольников О₁Аb, O₁AP, O₂Ba и O₂BP, получаем

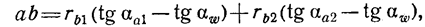
где a_a1 и a_а2 — углы профиля зуба у вершин, определяемые из со­отношений:

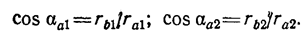
Отсюда коэффициент перекрытия

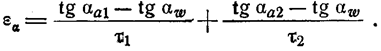(6.20)

Чем выше коэффициент перекрытия, тем лучше работает передача (меньше шум, вибрации). Увеличение коэффициента перекрытия может быть достигнуто применением косозубых колес (рис.6.20). В этом случае

e 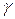=e _a + e _β (6.21)

где — e _β коэффициент осевого перекрытия.

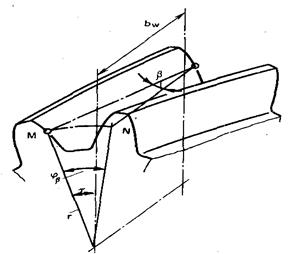
Коэффициент осевого перекрытия — отношение угла осевого перекрытия φ_β (угла поворота зубчатою колеса косозубой цилиндрической пере­дачи, при котором общая точка контакта зубьев перемещается но линии зуба этого колеса от одного из торцов, ограни­чивающих рабочую ширину венца, до другого) к его угловому шагу τ:

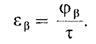
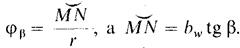(6.22)

Чем больше угол наклона линии зуба β, тем можно получить большую вели­чину e_β при той же рабочей ширине венца.

Увеличениеe_βпозволяет повысить несущую способность, плавность работы передачи, уменьшить шум, но приводит к возрастанию скорости скольжения контактных точек вдоль линии зуба и осевой составляющей силы в зацеплении.

Наименьшее число зубьев. При проектирова­нии зубчатых передач часто сталкиваются с проблемой габаритов пере­дачи. Как было показано выше, размеры передачи зависят от ее модуля и числа зубьев колес. Величина модуля определяется из условий проч­ности передачи. Беспредельное уменьшение габарита за счёт уменьше­ния числа зубьев невозможно, т.к. при некотором числе зубьев насту­пают нарушения нормальной работы передачи.

Наименьшее число зубьев, обеспечивающее нормальную работу пере­дачи, определяется из условия предотвращения заклинивания или под­резания ножки зуба шестерни головкой зуба колеса.

Эти явления могут происходить в тех случаях, когда длина актив­ной части линии зацепления больше расстояния между точками касания основных окружностей с линией зацепления (предельные точки).

Если такая картина наблюдается при нарезании зубьев, то проис­ходит подрезание ножки зуба, т.е. зуб ослабляется в опасном сечении, что может привести к выходу зацепления из строя.

Если увеличенная длина активной части линии зацепления наблюдается в работающей передаче, то происходит заклинива­ние, в результате чего — повышенный износ и разрушение зуба.

Установим условие отсутствия подрезания.

Рассмотрим DО₁MO₂ (рис. 6.16). Условие отсутствия подрезания

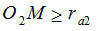
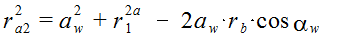(6.23)

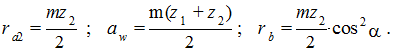
то, подставив полученные выражения в (6.23), получим

(r₂+2) 2 =(r₁+r₂) 2 +r 2 ₁cos 2 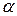_w-2(r₁+r₂)r₁cos 2 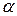_w (6.24)

Так как 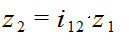, то

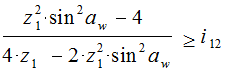(6.25)

Подставляя в (6.25) различные значения a_w и i₁₂ получают z_1min, при котором еще нет подрезания зубьев.

i12	z1min
aw = 20°	aw = 15°
5. 6
7. 12
13.

Обычно для нормального зубчатого зацепления с углом a_w = 20° принимают z_1min = 17.

Устранение подрезания при z > 1.

Угловая и высотная коррекция пу­тем смещения нормального инструмента.

Такая коррекция производится нормальным инструментом при на­резании зубчатого колеса методом обкатки. Определим требуемую вели­чину смещения инструмента, обеспечивающую нарезание зуба без под­резания (абсолютное смещение).

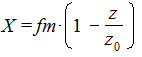(6.26)

где H = f× m — расстояние от средней линии инструмента (модуль­ной рейки) до точки, которой осуществляется подрезание. Следовательно

(6.27)

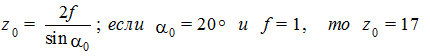
Тогда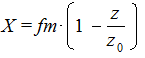

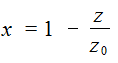
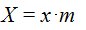(6.28)

Если Х > 0 , то смещение положительное и колеса обозначают­ся К+. Особенность такого зацепления — повышенный угол зацепле­ния и увеличенное межцентровое расстояние.

Иногда коррекцию зубчатых колес производят при z_min > 17 для того, чтобы вписаться в заданное межосевое расстояние. При этом применяется коррекция методом смещения нормального инструмента.

При использовании указанного метода, диаметр делительной окруж­ности остается неизменным, а диаметр начальной окружности увеличи­вается (при положительном) или уменьшается (при отрицательном) на 2 величины абсолютного смещения инструмента.

Коррекция может производиться так же для выравнивания коэффициентов удельного скольжения. В этом случае коэффициенты смещения инструмента выбираются по справочным таблицам.

Вопросы для самоконтроля

I. Какая кривая называется эвольвентной ?

2. Задайтесь модулем m и числами зубьев z₁ и z₂ пары зубчатых колес и постройте графически картину зацепления.

3. Что такое коэффициент перекрытия ? Каково его минимальное значение, необходимое для нормальной работы передачи ?

4. Чем определяется наименьшее число зубьев, обеспечивающее нормальную работу передачи ?

5. Как устранить подрезание ножки зуба при z