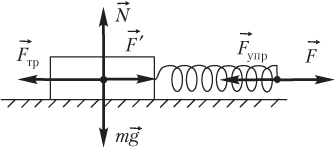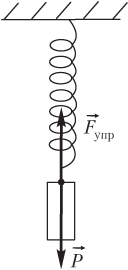Сила пружины при предварительной деформации что это?
Конструкция и расчет пружин
Пружины сжатия навиваются из круглой проволоки с зазором между витками. Они используются в тех случаях, когда нужны сравнительно большие деформации. Отношение максимального перемещения одного витка пружины к диаметру проволоки s3 /d = 0,3. 0,8.
Использование круглого сечения связано с тем, что оно лучше других работает на кручение при нагружении. Для обеспечения работоспособности узлов с пружинами сжатия при конструировании необходимо выполнить ряд требований:
- ? контакт между торцевыми витками и опорными деталями должен осуществляться на плоской поверхности, перпендикулярной к оси пружины;
- ? площадь контакта должна (по возможности) представлять собой полное кольцо для избежания дополнительного нагружения от изгиба;
- ? конструкция торцевых витков должна обеспечить правильное центрирование пружины в опорных элементах деталей.
Обеспечение этих условий достигается осадкой 0,75.. Л торцевых витков с каждой стороны и шлифовкой торцев пружин на плоскость, а также наличием в узле деталей, центрирующих ее с обоих концов.

На рис. 17.1 приведена пружина сжатия с вариантом за- концовки, при котором крайний виток пружины поджат на 3 /4 и сошлифован на 3 /4 дуги окружности (к — зазор между концом опорного витка толщи- ной 5 и соседним рабочим вит- ис ’ * ком). На рис. 17.1 t — шаг пру
жины в свободном состоянии; Н3, Н0 — длина пружины при максимальной силе F3 и в свободном состоянии (F = 0); —
перемещение пружины под действием силы Ft; h — рабочий ход; F3 — сила пружины при максимальном перемещении з3; Fx — сила пружины при предварительном перемещении 8г; F2 — сила пружины при рабочей деформации s2.
Пружины характеризуются следующими геометрическими параметрами: диаметром проволоки d; средним диаметром пружины D; шагом витка t; углом подъема витков a, tg а = = t/(nD); длиной рабочей части пружины Нр; числом рабочих витков п — Hp/tf Нр = Н0 — НК, Нк = 1,5d (витки сошлифова- ны с каждого конца на 0,75d).
В ГОСТах 13766—86— 13775—86 на пружины сжатия регламентируются параметры витка пружины; диаметр проволоки 3 c) = Gd/(8ci 3 ), где с =
= ——- — жесткость пружины. п

Тарельчатые пружины предназначены для восприятия больших сжимающих сил при малых перемещениях. Эти пружины изготавливаются в виде тарелок без днищ из стали марки 60С2А, твердость материала 45,5. 51,5 HRC3 (рис. 17.4, а, где D, Dx — наружный и внутренний диаметры пружины). Тарельчатые пружины располагаются в комплекте из нескольких штук (см. табл. 17.1). Рабочая деформация пружины s =
Пружины кручения. К ним относятся витые, плоские спиральные пружины и торсионы. При использовании пружин кручения нужно учитывать то, что плоские спиральные пружины имеют меньшие габариты и большую податливость, чем витые цилиндрические, но выдерживают меньшие крутящие моменты. Торсионы имеют малые радиальные размеры, но большую длину и воспринимают значительные крутящие моменты при небольшой податливости (рис. 17.4, б, где 3 — за- концовка). Витые цилиндрические пружины кручения навиваются из проволоки круглого сечения с зазором 0,2. 0,5 мм между витками, во избежание трения между ними. Примеры оформления концов пружины для восприятия крутящего момента приведены на рис. 17.3, б. При установке пружина должна центрироваться. Кроме того, диаметр центрирующего элемента должен выбираться так, чтобы при скручивании пружины, когда ее диаметр уменьшается, между витками пружины и центрирующей поверхностью оставался зазор. При действии крутящего момента основная нагрузка на виток связана с его изгибом.
витой цилиндрической пружины кручения
Исходные данные: вращающий момент пружины при предварительном закручивании 7, а при рабочем Т2, рабочий угол закручивания 0 = 4 0/[18O • 64 • (Т2 — Tt)i] = 0,27-10
s Ed*Q/[(T2 — Tx)i]; жесткость пружины с * (Т2 — Тх)/0; углы закручивания пружины при нагрузке вращающим моментом Т,
Плоские спиральные пружины (см. табл. 17.1) изготавливаются из тонкой высококачественной углеродистой стальной ленты. Они применяются в качестве пружинных двигателей, аккумулирующих энергию при заводе. Благодаря высокой гибкости ленты пружина аккумулирует значительное количество энергии и позволяет осуществить угол поворота валика до нескольких десятков оборотов.
Торсион представляет собой цилиндрический стержень с законцовками 3 на торцах для его крепления (рис. 17.4, б). Обычно заделка осуществляется с помощью эвольвентного шлицевого соединения. Использование торсионов особенно целесообразно в случае соединения полых соосных деталей, когда конструкция позволяет использовать торсионы значительной длины. В этих случаях угол закручивания может достигать нескольких десятков градусов. Для снижения массы торсионы часто делаются полыми. Эффективно изготавливать торсионы из титановых сплавов, что не только снижает массу, но и благодаря меньшему модулю упругости, чем у стали, обеспечивает больший угол поворота.
Сила упругости

О чем эта статья:
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
- Деформация растяжения
- Деформация сжатия
- Деформация сдвига
- Деформация при кручении
- Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно упругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
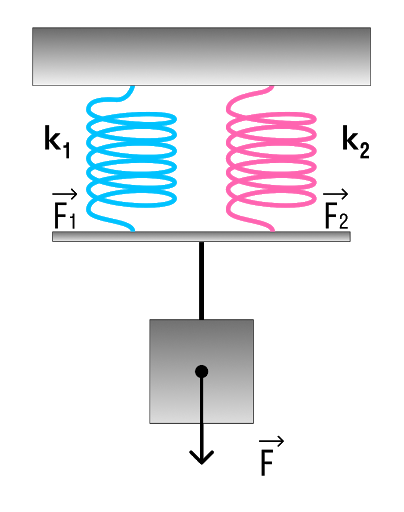
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
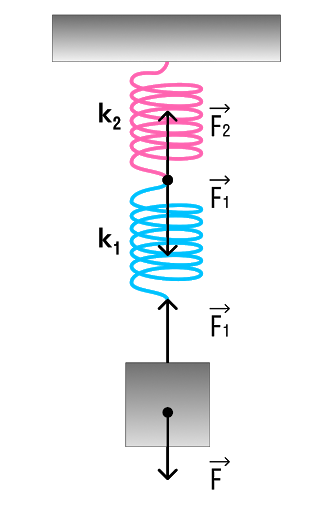
При последовательном соединении общая жесткость двух пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
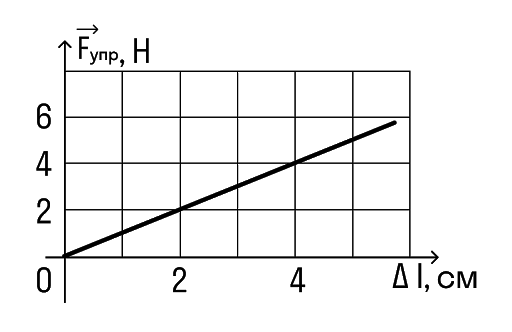
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
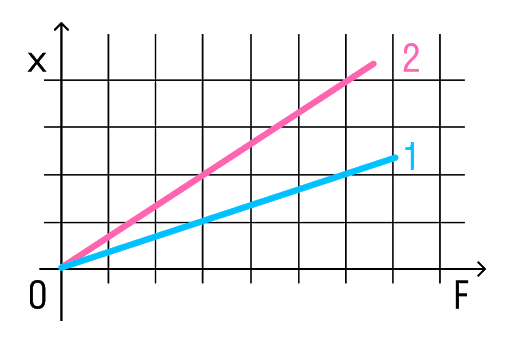
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
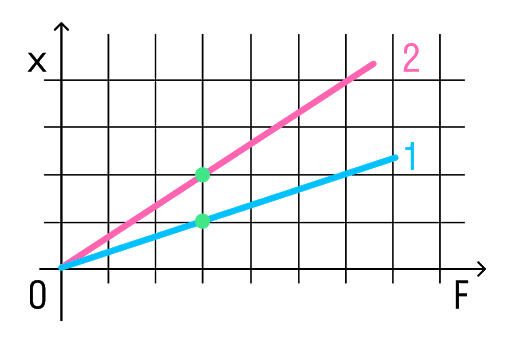
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.


Каникулы со смыслом в Skysmart для детей 4-17 лет
ГОСТ 13764-86 Пружины винтовые цилиндрические сжатия и растяжения из стали круглого сечения. Классификация
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
ПРУЖИНЫ ВИНТОВЫЕ ЦИЛИНДРИЧЕСКИЕ
СЖАТИЯ И РАСТЯЖЕНИЯ ИЗ СТАЛИ КРУГЛОГО СЕЧЕНИЯ
Классификация
Cylindrical helical compression (tension) springs made of round steel. Classification
Дата введения 01.07.88
Настоящий стандарт распространяется на пружины, предназначенные для работы в неагрессивных средах при температуре от минус 60 °С до плюс 120 °С.
1 . Пружины разделяются на классы, виды и разряды в соответствии с указанными в табл. 1 и 2 .
Выносливость NF (установленная безотказная наработка), циклы, не менее
Инерционное соударение витков
Сжатия и растяжения
Сжатия и растяжения
Циклическое и статическое
1. Отсутствие соударения витков у пружин сжатия определяется условием:
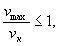
где v max — наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке, м/с;
vк — критическая скорость пружины сжатия (соответствует возникновению соударения витков пружины от сил инерции), м/с.
2. Значения выносливости не распространяются на зацепы пружин растяжения.
3. Критериями отказа в условиях эксплуатации является невыполнение требований ГОСТ 16118 .
Сила пружины при максимальной деформации, F 3 , H
Диаметр проволоки (прутка) d , мм
Твердость после термообработки, HRC э
Максимальное касательное напряжение при кручении t 3 , МПа
Требование к упрочнению
Стандарт на основные параметры витков пружин
Стандарт на заготовку
Одножильные сжатия и растяжения
По ГОСТ 1050 и ГОСТ 1435
Проволока класса I по ГОСТ 9389
Для повышения циклической стойкости рекомендуется упрочнение дробью
Проволока классов II и IIА по ГОСТ 9389
51ХФА-Ш по ГОСТ 14959
Проволока по ГОСТ 1071
60С2А; 65С2ВА; 70С3А по ГОСТ 14959
Проволока по ГОСТ 14963
51ХФА по ГОСТ 14959
Проволока по ГОСТ 14963
60С2А; 65С2ВА; 70С3А; 60С2; 60С2ХА; 60С2ХФА; 51ХФА по ГОСТ 14959
Сталь горячекатаная круглая по ГОСТ 2590
Одножильные сжатия и растяжения
По ГОСТ 1050 и ГОСТ 1435
Проволока класса I по ГОСТ 9389
Проволока классов II и IIА по ГОСТ 9389
51ХФА-Ш по ГОСТ 14959
Проволока по ГОСТ 1071
60С2А; 65С2ВА по ГОСТ 14959
Проволока по ГОСТ 14963
65Г по ГОСТ 14959
Проволока по ГОСТ 2771
51ХФА по ГОСТ 14959
Проволока по ГОСТ 14963
60С2А; 60С2; 65С2ВА; 70С3А; 51ХФА; 65Г; 60С2ХФА; 60С2ХА по ГОСТ 14959
Сталь горячекатаная круглая по ГОСТ 2590
По ГОСТ 1050 и ГОСТ 1435
Проволока класса I по ГОСТ 9389
60С2А; 65С2ВА; 70С3А по ГОСТ 14959
Проволока по ГОСТ 14963
Обязательно упрочнение дробью
60С2А; 65С2ВА; 70С3А по ГОСТ 14959
Сталь горячекатаная круглая по ГОСТ 2590
1. Максимальное касательное напряжение при кручении t3 приведено с учетом кривизны витков.
2. Допускается использование основных параметров витков по ГОСТ 13766 , ГОСТ 13767 , ГОСТ 13770 , ГОСТ 13771 для пружин растяжения с предварительным напряжением.
Класс пружин характеризует режим нагружения и выносливости, а также определяет основные требования к материалам и технологии изготовления.
Разряды пружин отражают сведения о диапазонах сил, марках применяемых пружинных сталей, а также нормативах по допускаемым напряжениям.
(Измененная редакция, Изм. № 1).
2 . В стандарт включены дополнительные требования, которые приведены в приложениях 1 — 3 .
ПРИЛОЖЕНИЕ 1
Справочное
КРАТКИЕ СВЕДЕНИЯ О ВЫНОСЛИВОСТИ И СТОЙКОСТИ ЦИКЛИЧЕСКИХ И СТАТИЧЕСКИХ ПРУЖИН
При определении размеров пружин необходимо учитывать, что при v max > v к , помимо касательных напряжений кручения, возникают контактные напряжения от соударения витков, движущихся по инерции после замедления и остановок сопрягаемых с пружинами деталей. Если соударение витков отсутствует, то лучшую выносливость имеют пружины с низкими напряжениями t 3 , т.е. пружины I класса, промежуточную — циклические пружины II класса и худшую — пружины III класса.
При наличии интенсивного соударения витков выносливость располагается в обратном порядке, т.е. повышается не с понижением, а с ростом t 3 . В таком же порядке располагается и стойкость, т.е. уменьшение остаточных деформаций или осадок пружин в процессе работы.
Средствами регулирования выносливости и стойкости циклических пружин в рамках каждого класса при неизменных заданных значениях рабочего хода служат изменения разности между максимальным касательным напряжением при кручении t 3 и касательным напряжением при рабочей деформации t 2 .
Возрастание разности t 3 — t 2 обусловливает увеличение выносливости и стойкости циклических пружин всех классов при одновременном возрастании размеров узлов. Уменьшение разности t 3 — t 2 сопровождается обратными изменениями служебных качеств и размеров пространств в механизмах для размещения пружин.
Для пружин I класса расчетные напряжения и свойства металла регламентированы так, что при v max / v к v max / v к v max / v к и величинах относительного инерционного зазора пружин d не более 0,4 [формула ( 1) ГОСТ 13765] характеризуются ограниченной выносливостью, поскольку они рассчитаны на предельно высокие касательные напряжения кручения, к которым при v max / v к > l добавляются контактные напряжения от соударения витков.
Статические пружины, длительно пребывающие в деформированном состоянии и периодически нагружаемые со скоростью v max менее v к , относятся ко II классу. Вводимые стандартом ограничения расчетных напряжений и свойств проволоки (ГОСТ 13764, табл. 2) обеспечивают неограниченную стойкость статических пружин при остаточных деформациях не более 15 % величины максимальной деформации s 3 .
Допустимые остаточные деформации статических пружин регламентируются координацией сил пружины при рабочей деформации s 3 на силовых диаграммах, причем увеличение разности F 3 — F 2 способствует уменьшению остаточных деформаций.
Технологические средства регулирования выносливости и стойкости пружин определяются документацией на технические условия.
ПРИЛОЖЕНИЕ 2
Справочное
КРАТКИЕ СВЕДЕНИЯ О МАТЕРИАЛАХ
Имеющиеся в промышленности марки пружинной стали характеризуются следующими свойствами и условиями применения.
Проволока класса I по ГОСТ 9389. Высокая разрывная прочность. Наличие больших остаточных напряжений первого рода (от волочения и навивки) обусловливает появление остаточных деформаций пружин при напряжениях t 3 > 0,32 Rm . При v max > v к остаточные деформации высоки независимо от применения операции заневоливания. В связи с указанным проволока класса I по ГОСТ 9389 назначается для пружин III класса в виде трехжильных тросов.
Проволока классов II и II А по ГОСТ 9389. Отличается от проволоки класса I уменьшенной прочностью при разрыве и повышенной пластичностью. Применяется для изделий, работающих при низких температурах, а также для пружин растяжения со сложными конструкциями зацепов. Проволока класса II А отличается от проволоки класса II более высокой точностью размеров, уменьшением вредных примесей в металле и дальнейшим повышением пластичности.
Сталь марки 65Г. Повышенная склонность к образованию закалочных трещин. Применяется с целью удешевления продукции для изделий массового производства в случаях, когда поломки пружин не вызывают нарушения функционирования деталей механизмов и не связаны с трудоемкими заменами.
Сталь марки 51ХФА. Повышенная теплоустойчивость. Закаливается на твердость не более 53,5 HRC э . В результате высоких упругих и вязких свойств служит лучшим материалом для пружин I класса.
Сталь марок 60С2А, 60С2. Высокие упругие и вязкие свойства. Повышенная склонность к графитизации и недостаточная прокаливаемость при сечениях d > 20 мм. Широкая применимость для пружин I и II классов. Для пружин III класса назначается при v max £ 6 м/с.
Сталь 60С2ХФА. Высокая прокаливаемость, малая склонность к росту зерна и обезуглероживанию при нагреве (по сравнению со сталью 60С2А), повышенные вязкость, жаропрочность и хладостойкость, хорошая циклическая прочность и релаксационная стойкость в широком диапазоне циклических изменений температур. Предпочтительное применение в сечениях проволоки от 30 мм и выше.
Сталь марки 65С2ВА. Высокие упругие свойства и вязкость. Повышенная прокаливаемость. Служит лучшим материалом для пружин III класса. Применяется при v max > 6 м/с.
Сталь марки 70С3А. Повышенная прокаливаемость. Обладает склонностью к графитизации. Преимущественное применение при диаметрах проволоки d > 20 мм. Заменителем служит сталь 60С2Н2А.
Примечание. Преимущественное практическое использование пружин из стали марки 51ХФА определяется интервалом температур от минус 180 до плюс 250 °С, из стали марки 60С2ХФА от минус 100 до плюс 250 °С, из проволоки класса IIA по ГОСТ 9389 от минус 180 до плюс 120 °С, из стали марок 65Г, 70С3А, 60С2А, 65С2ВА и из проволоки класса I по ГОСТ 9389 от минус 60 до плюс 120 °С. В случаях использования пружин при более высоких температурах рекомендуется учитывать температурные изменения модуля.
(Измененная редакция, Изм. № 1).
ПРИЛОЖЕНИЕ 3
Справочное
КРАТКИЕ СВЕДЕНИЯ О НАЗНАЧЕНИИ ВЫСОКОЙ ТВЕРДОСТИ ДЛЯ ПРУЖИН III КЛАССА
Установлено, что пружины сжатия, работающие в режиме интенсивного соударения витков, преждевременно выходят из строя, главным образом, по причине поломок опорных витков, а также по причине быстрой потери сил в результате остаточных деформаций.
Назначение высокой твердости способствует возрастанию упругих свойств и предела прочности Rm пружинных материалов, в результате чего остаточные деформации резко уменьшаются и благодаря этому пружины более продолжительное время работают без поломок и без недопустимых потерь сил.
У применяемых марок стали безопасным для работоспособности пружин III класса является интервал твердости HRC э 53,5 . 58,0, однако условием для этого служит обязательное применение дробеструйной обработки независимо от требуемых норм выносливости. Важной предпосылкой назначения высокой твердости служит также всемерное сокращение периодов нагрева для закалки и установление продолжительности отпуска на заданную твердость не менее 45 мин при нагреве в жидких ваннах и не менее 1 ч при нагреве в воздушной среде.
Все пружины, закаливаемые на высокую твердость, в зависимости от уровня требований к стабильности размеров и сил, а также с целью контроля дефектов металла рекомендуется подвергать заневоливанию до соприкосновения витков, также копровой или стендовой отбивке.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
Б.А. Станкевич (руководитель темы) ; О.Н. Магницкий, д-р. техн. наук ; А.А. Косилов; Б.Н. Крюков; Е.А. Караштин, канд. техн. наук
2 . УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 19.12.86 № 4007
3 . Стандарт полностью соответствует СТ СЭВ 5616-86
4 . ВЗАМЕН ГОСТ 13764-68
5 . ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
Физика
Силы упругости возникают при деформации тел.
Вычисление силы упругости производится по закону Гука :
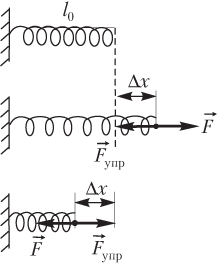
где k — коэффициент жесткости (упругости) пружины; Δ x = | l − l 0 | — абсолютная деформация (растяжения или сжатия) пружины, l 0 — длина пружины в недеформированном состоянии, l — длина растянутой (или сжатой) пружины.
Направление силы упругости F → упр (рис. 2.9) противоположно направлению силы, вызывающей деформацию:
Относительная деформация определяется отношением:
ε = Δ x l 0 или ε = Δ x l 0 ⋅ 100 % ,
где Δ x = | l − l 0 | — абсолютная деформация (растяжения или сжатия) пружины, l 0 — длина недеформированной пружины, l — длина растянутой (сжатой) пружины.
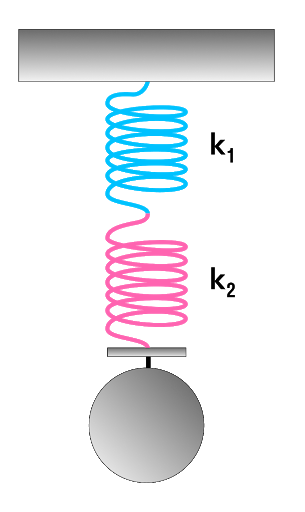
Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины , но разной жесткости вычисляется для последовательного соединения по формуле (рис. 2.10)
1 k = 1 k 1 + 1 k 2 + . + 1 k N ;
где k 1 , k 2 , . k N — коэффициенты жесткости (упругости) этих пружин.
Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины , но разной жесткости (рис. 10), вычисляется для параллельного соединения по формуле (рис. 2.11)
k = k 1 + k 2 + . + k N ,
где k 1 , k 2 , . k N — коэффициенты жесткости (упругости) этих пружин.
- для последовательного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k 0 :
для параллельного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k 0 :
Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.
Решение. Величина силы упругости, действующей на пружину, определяется формулой
F упр = k общ ∆ x ,
где k общ — коэффициент жесткости составной пружины; ∆ x — указанное в условии задачи растяжение пружины.
Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:
Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:
k общ = F Δ x = 12 4,0 ⋅ 10 − 2 = 300 Н/м.
Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:
- для первой пружины
- для второй пружины
- для третьей пружины
так как указанные коэффициенты по условию задачи соотносятся между собой как
k 1 : k 2 : k 3 = 1 : 2 : 3.
Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k 1 , k 2 , k 3 :
1 k общ = 1 k 1 + 1 k 2 + 1 k 3 = 1 k + 1 2 k + 1 3 k = 11 6 k , или k общ = 6 k 11 .
Найденное ранее значение k общ = 300 Н/м позволяет рассчитать k = 550 Н/м.
Тогда коэффициенты жесткости каждой из пружин имеют значения:
- для первой пружины
- для второй пружины
k 2 = 2 k = 1100 Н/м;
- для третьей пружины
k 3 = 3 k = 1650 Н/м.
Пример 17. Вычислить абсолютную деформацию пружины с коэффициентом жесткости 100 Н/м, присоединенной к бруску, лежащему на горизонтальной поверхности, в момент начала скольжения бруска по поверхности. Сила, вызывающая скольжение бруска, прикладывается к пружине. Коэффициент трения между бруском и поверхностью равен 0,1. Масса бруска составляет 1,0 кг.
Решение. На рисунке показаны силы, действующие на брусок.
Абсолютную деформацию пружины рассчитаем по формуле
где F упр = F — модуль силы упругости, возникающей в пружине (величина силы упругости равна величине приложенной силы); k — коэффициент жесткости пружины.
Со стороны пружины на брусок действует сила, модуль которой совпадает с силой упругости:
В момент начала скольжения величина силы трения равна силе, приложенной к бруску в направлении движения:
где µ — коэффициент трения; N = mg — модуль силы нормальной реакции опоры.
Поэтому величина силы упругости может быть вычислена по формуле
Из исходного уравнения следует, что величина деформации пружины в момент начала скольжения определяется выражением
Расчет позволяет определить ее значение:
Δ x = 0,1 ⋅ 1,0 ⋅ 10 100 = 10 − 2 м = 1,0 см .
Пример 18. Вычислить массу груза, подвешенного к пружине жесткостью 250 Н/м, если известно, что относительная деформация пружины составляет 25 %. Длину нерастянутой пружины считать равной 100 мм.
Решение. Проиллюстрируем условие задачи рисунком.
Сила упругости определяется формулой
где k — коэффициент жесткости (упругости) пружины; ∆ x = l − l 0 — абсолютная деформация пружины (величина ее растяжения под действием груза); l 0 — длина недеформированной пружины; l — длина пружины в деформированном состоянии.
Из определения относительной деформации
где ε = 0,25 — относительная деформация (в долях).
С учетом значения относительной деформации формула для вычисления силы упругости принимает вид:
F упр = k ε l 0 = 0,25 k l 0 .
С другой стороны, сила упругости, возникающая в пружине, численно равна весу тела, вызвавшего деформацию пружины:
где m — масса тела; g — модуль ускорения свободного падения.
Таким образом, имеем равенство
позволяющее вычислить массу груза, подвешенного к пружине:
m = 0,25 k l 0 g = 0,25 ⋅ 250 ⋅ 0,100 10 = 0,625 кг = 625 г .
Определение характеристик витых пружин растяжения и сжатия
Лабораторная работа 26
Цель работы: исследование зависимости изменения деформации пружин растяжения и сжатия от геометрических и силовых параметров, ознакомление с типами пружин, их конструкциями.

Рис. 4.6.1. Классификация пружин
Краткие теоретические сведения
Пружины используются в различных машинах и приборах. С их помощью создается постоянная сила нажатия и натяжения между деталями машины или прибора (во фрикционных передачах, муфтах, тормозах и т. п.), осуществляются виброизоляция, автоматизация ударов (амортизаторы, буферы, рессоры и т. п.), аккумулирование энергии с последующим использованием пружины как двигателя (часовые и прочие пружины), измерение сил (в динамометрах и других измерительных приборах).
По форме и конструкции пружины бывают витые, цилиндрические, конические, тарельчатые, кольцевые, стержневые, блочные, спиральные, плоские, рессоры.
По виду нагружения различают пружины растяжения, сжатия, кручения и изгиба.
Примерная классификация пружин по указанным признакам приведена на рис. 4.6.1.
В машиностроении чаще используются пружины из круглой проволоки, так как они дешевле других, лучше работают на кручение. Пружины свитками квадратного и прямоугольного сечения (рис. 4.6.1, в) применяют при больших нагрузках, а также когда из-за сложности навивки пружины нужно вырезать из трубы. Это пружины сжатия. В массовом и крупносерийном производстве витые пружины изготавливают на специальных станках- автоматах. В остальных случаях пружины производят на токарных станках.
Технология навивки зависит от индекса изготовляемой пружины. Для пружин с витками круглого сечения индекс с = D/d, где D — средний диаметр пружины; d — диаметр проволоки. Чем меньше индекс с, тем труднее навивать пружины. Обычно с = 4-12.
Пружины заневоливают с целью повышения их несущей способности. Заневоливание — это технологический прием, заключающийся в том, что, пружину на определённое время (6-48 ч) предельно нагружают до соприкосновения витков; при этом в наружных наиболее нагруженных слоях витков возникают остаточные деформации (остаточные напряжения), по знаку противоположные рабочим, в результате чего наибольшие суммарные напряжения снижены.
Пружины сжатия навивают так называемой открытой навивкой, обеспечивающей определенный зазор 5 между витками (рис. 4.6.1, б, в, г).
Пружины растяжения делают с закрытыми витками, плотно прилегающими друг другу (рис. 4.6.1, а).
Чтобы витки плотно прилегали, проволоку в процессе навивания натягивают, подвергая её тем самым упругой деформации растяжения. Такая навивка называется закрытой. При снятии готовой пружины с оправки происходит упругая отдача материала, пружина раздается в диаметре,
и витки настолько плотно прилегают друг к другу, что вся пружина приобретает предварительное натяжение, вследствие чего увеличивается её несущая способность.
Пружины растяжения диаметром до 3 мм обычно выполняют с прицепами в виде изогнутых витков (рис. 4.6.2, а, б). В местах отгиба концентрируются напряжения, что снижает несущую способность пружины. Поэтому для ответственных сильно напряженных пружин применяют прицепы с коническим переходом (рис.4.6.2, в), закладные прицепы с заделкой (рис. 4.6.2, г) и крепления с помощью пластин (рис. 4.6.2, д). Наиболее совершенно крепление ввертными винтовыми пробками с крючками (рис.4.6.2, ё) для пружин с диаметром проволоки свыше 5 мм.
Для того чтобы нагрузка на пружину сжатия передавалась по оси пружины и чтобы уменьшить напряжения изгиба концевых винтов, их поджимают к соседним виткам, а торцевые поверхности пружины шлифуют перпендикулярно её оси.

Рис. 4.6.2. Прицепы пружин растяжения: а, б- изогнутые витки; в — с коническим переходом; г, д- закладные; е — ввертные винтовые пробки

Рис. 4.6.3. Способы установки пружин сжатия: а — без оправки; б — на оправке или в стакане; в — составные
Пружины сжатия, у которых HJD > 2,6 (Н0 — длина пружины в свободном состоянии), в процессе работы могут выпучиваться (рис. 4.6.3, а), поэтому их необходимо ставить на оправки или монтировать в направляющих стаканах (рис. 4.6.3, в) (реже — большего числа) вложенных одна в другую цилиндрических пружин. Уменьшают габариты конструкции.
Применяются также многожильные пружины из двух, трёх и большего числа проволок, свитых в трос (см. сечения тросов на рис. 4.6.3, б),
Конические пружины могут иметь витки круглого (рис. 4.6.1, г) и прямоугольного сечений с большим отношением сторон. Последние навивают из полосовой стали и называют телескопическими (рис. 4.6.1, д).
Витые цилиндрические одножильные пружины из проволоки круглого сечения характеризуются следующими основными геометрическими параметрами (рис. 4.6.4): диаметр проволоки (сечение витка) средний диаметр пружины D; индекс пружины с; шаг витков t; угол подъёма витка а, tg а = t/nD; длина рабочей части пружины Hd число рабочих витков п.
Шаг витка, угол подъёма витков и длины рабочей части пружины рассматривают отдельно в ненагруженном и нагруженном состояниях.
Чем податливее должна быть пружина, тем большим берут индекс пружины с и число витков. Индекс пружины выбирают в независимости от диаметра проволоки в следующих пределах:
d, мм. до 2,5 3 . 5 6 . 12
с, мм . 5 . 12 4 . 10 4 . 9

Рис. 4.6.4. Расчётная схема витой пружины растяжения или сжатия
Увеличив индекс пружины, можно при той же жесткости сократить габариты пружины по длине за счёт увеличения диаметра, и, наоборот, уменьшив индекс пружины, можно уменьшить диаметр пружины за счёт увеличения длины.
Силовые факторы, действующие в любом поперечном сечении пружин растяжения и сжатия, сводятся к моменту М = FD/2, вектор которого перпендикулярен оси пружины и силе F, действующей вдоль оси пружины (рис. 4.6.4).
Силовые факторы, действующие в любом поперечном сечении пружин растяжения и сжатия, сводятся к моменту М = FD/2, вектор которого перпендикулярен оси пружины и силе F, действующей вдоль оси пружины (рис. 4.6.4).
Момент М раскладывается на крутящий Т и изгибающий Ми моменты:

В большинстве пружин угол подъема витков а 4. Детали машин
Окончание табл. 4.6.1
Параметры исследуемых пружин
Диаметр проволоки d, мм